64괘
우리가 배우고 있는 수학의 기원은 대부분이 서양에서 비롯되었는데, 순열과 조합은 동양에서 그 기 원을 찾을 수 있습니다. 순열에 대한 오래된 기록은 중국과 인도에서 발견되었습니다.
중국에서는 우주와 인간의 삶의 다양함을 설명하기 위하여 두 개의 효( -,-- )를 배열 하여 8괘와 64괘를 만들었는데, 두 개의 효의 다양한 배열은 역(易)의 기본 구조가 되었습니다. 특히 배열에 관하 여 흥미를 돋우는 소재인 마방진에 관한 기록은 1세기경 중국의 기록에서 찾아볼 수 있다고 합니다.
인도에서는 6세기경에 브라마굽타`(Brahmagupta ; 598~?665)가 n개의 원소를 가지는 집합의 원소를 재 배열하는 순열의 수가 n(n-1)(n-2)…2·1이라는 것을 알고 있었습니다. 그로부터 약 500년 후인 1150년경 에 바스카라(Bhaskara, A. ; 1114~1185(1193?)) 는 n개의 원소를 가지는 집합에서 k개의 원소를 가지 는 부분집합을 만들 수 있는 경우의 수가

이라는 것을 알고 있었던 것으로 여겨집니다. 그는 예술, 건축, 음악, 의학 등에서 순열의 개념을 발견하기 위해 노력하였던 것으로 알려져 있습니다.

로마 최후의 철학자 보이티우스
한편 고대 그리스나 로마 시대에는 순열을 본격적으 로 다루지 않은 것으로 추측됩니다. 다만 보이티우스 (Boethius A. M. S ; ?480~524)가 n개의 사건들 중에서 2개를 조합하는 경우의 수가

이 된다 는 것을 언급했을 뿐입니다.
중세 시대에 아라비아 인들과 유대 인들은 수학과 천 문학에 대하여 많이 연구했습니다. 예를 들어 랍비 벤 에즈 라(Ben Ezra, 1140년경)는 태양계의 행성들이 한 줄 로 합쳐지는 배열에 대하여 연구하였고, 토성이 다른 행성들과 가질 수 있는 위치 관계의 경우의 수를 찾으려고 노력했습니다. 특히 벤은 서로 다른 7개 중에서 2개를 택하는 조합의 수가 서로 다른 7개 중에서 5개를 택하 는 조합의 수와 같다는 것을 알고 있었습니다. 즉, 조합의 성질인
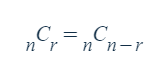
를 알고 있었던 것입니다. 그러나 그는 이런 내용들을 발표하지는 않았습니다.
거슨(Gerson, L. B.)은 1321년에“Maassei Choscheb”라는 책에서 서로 다른 n개 중에서 r개를 택하는 순열의 수와 조합의 수에 대한 일반적인 원리를 설명했습니다.
그로부터 몇 년 후 오렘(Oresme, N. ; ?1320~1382)은 서로 다른 6개 중에서 1개, 2개, 3개, 4개, 5개를 택하는 조합의 수들의 합, 즉
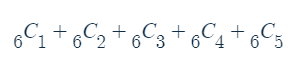
를 계산하였으며 구체적으로 조합의 수를
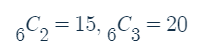
으로 계산하였습니다.

이탈리아 수학자 루카 파촐리
순열과 조합에 대한 보다 체계적인 연구는 1494년 파촐리(Pacioli, L. ; 1445~1517)가 지은“Summa de Arithmetica”에서 찾아볼 수 있습니다. 이 책에서 파 촐리는 몇 명의 사람들이 탁자에 앉는 경우의 수를 구 하는 방법을 설명했습니다. 또 1523년 이탈리아의 수학자인 타르탈리아 (Tartaglia, N.` F. ; 1499~1557)는 주사위를 던지 는 경우에 순열과 조합의 이론을 처음으로 적용하였고, 1540년 영국에서는 버클리(Buckley, W.)가 n개 중 에서 r개를 택하는 조합의 특별한 경우를 예로 들 었습니다.
16세기의 랍비 모세스 코르도베로(Moses Cordovero ; 1522~1570)는“Pardes Rimmonim” 을 저술하였는데, 여기서 그는 순열과 조합에 대한 흥미 로운 사례와 몇 가지 일반적인 내용을 언급하고 있습니다. 비슷한 시기에 부테오(Buteo)는 4개의 주사위를 던질 때 일어날 수 있는 경우의 수와 오늘날 번호 열쇠와 원 통형 열쇠 번호의 가능한 조합의 수를 예로 들었습니다.
오늘날과 같은 조합의 수
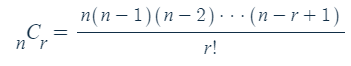
을 일반적인 방법으로 기술한 사람은 1634년 프랑스의 수학자인 해리건(He´ rigone, P. ; 1580~1643)입니다.