<하양짱샘수학과외>절대부등식 - 코시-슈바르츠 부등식

의의 실수 a, b, x, y 에 대하여 부등식

$\left(a^2+b^2\right)\left(x^2+y^2\right)\ge \left(ax+by\right)^2$(a2+b2)(x2+y2)≥(ax+by)2​

이 항상 성립한다. 이 부등식은 코시(Cauchy, A. L. ; 1789 ~ 1857)에 의해 제시되고 슈바르츠(Schwarz, H. A. ; 1843 ~ 1921)에 의해 더욱 발전되었기에, 그들의 이름을 따서 코시-슈바르츠 부등식이라고 한다.

​

가장 기본적이면서도 매우 강력한 부등식으로, 다양하게 일반화되고 있으며 선형대수학, 해석학, 확률론 등 여러 수학 분야에서 사용된다.

​

산술평균-기하평균 부등식은 양수의 범위에서만 사용할 수 있는 데 비해, 코시-슈바르츠 부등식은 실수, 복소수, 벡터 등 더 넓은 범위에서 성립한다.

​

임의의 실수 a, b, x, y 에 대하여 부등식

$\left(a^2+b^2\right)\left(x^2+y^2\right)\ge \left(ax+by\right)^2$(a2+b2)(x2+y2)≥(ax+by)2​

이 성립한다. 단, 등호는

$ay-bx=0$ay−bx=0​

일 때 성립한다.

​

임의의 실수 에 대하여

$\left(a^2+b^2\right)\left(x^2+y^2\right)-\left(ax+by\right)^2$(a2+b2)(x2+y2)−(ax+by)2​

$=a^2x^2+a^2y^2+b^2x^2+b^2y^2-\left(a^2x^2+2abxy+b^2y^2\right)$=a2x2+a2y2+b2x2+b2y2−(a2x2+2abxy+b2y2)​

$=a^2y^2-2abxy+b^2x^2$=a2y2−2abxy+b2x2​

$=\left(ay-bx\right)^2\ge 0$=(ay−bx)2≥0​

이므로

$\left(a^2+b^2\right)\left(x^2+y^2\right)\ge \left(ax+by\right)^2$(a2+b2)(x2+y2)≥(ax+by)2​

이 성립한다.단, 등호는

$ay-bx=0$ay−bx=0​

일 때 성립한다.

​

코시-슈바르츠 부등식의 기하학적 증명

앞서 나온 대수적인 증명은 코시-슈바르츠 부등식을 증명할 때 널리 사용된다.

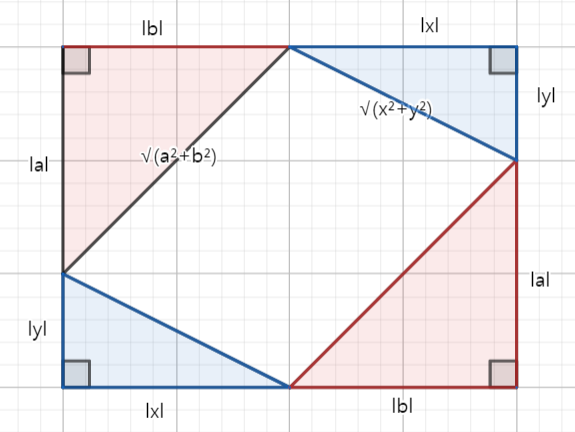
이와 다르게 로저 넬슨(Nelson, R. B.)은 도형을 이용하여 코시-슈바르츠 부등식이 성립함을 직관적으로 보여주는 기하적 증명 방법(geometric proof)을 제시하였다.

 

(a) (b)

(a)의 하얀색 평행사변형은 변의 길이가 각각

$\sqrt{a^2+b^2},\ \sqrt{x^2+y^2}\ $√a2+b2, √x2+y2 ​

인 직각삼각형으로 둘러싸여 있다.

네 직각삼각형과 하얀색 평행사변형으로 이루어진 큰 직사각형은, 가로와 세로의 길이는 각각

$\left|\combi{a}\right|+\left|y\right|,\ \ \left|\combi{b}\right|+\left|x\right|$|a|+|y|,  |b|+|x|​

이므로 큰 직사각형의 넓이는

$S=\left(\left|\combi{a}\right|+\left|y\right|\right)\left(\ \left|\combi{b}\right|+\left|x\right|\right)$S=(|a|+|y|)( |b|+|x|)​

이다. 이때 (a)의 넓이는 (b)의 넓이 보다 항상 작거나 같다.

∵ 4개의 직사각형의 넓이는 (a)일때와 (b)일때 변함이 없지만 (a)의 평행사각형의 넓이는 (b)의 직사각형의 넓이 보다 작거나 같다.

(a)의 평행사각형의 넓이는

$\sqrt{a^2+b^2}\ \sqrt{x^2+y^2}\sin \theta $√a2+b2 √x2+y2sinθ​

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \sin \theta \le 1$              sinθ≤1​

(b)의 직사각형의 넓이는

$\sqrt{a^2+b^2}\ \sqrt{x^2+y^2}$√a2+b2 √x2+y2​

이다.

(a)와 (b)의 넓이를 비교하면

$\left(\left|\combi{a}\right|+\left|y\right|\right)\left(\ \left|\combi{b}\right|+\left|x\right|\right)\le 2\left(\combi{\frac{1}{2}\left|\combi{a}\right|\left|\combi{b}\right|+\frac{1}{2}\left|\combi{x}\right|\left|\combi{y}\right|}\right)+\sqrt{a^2+b^2}\sqrt{x^2+y^2}$(|a|+|y|)( |b|+|x|)≤2(12​|a||b|+12​|x||y|)+√a2+b2√x2+y2​

$\left|\combi{a}\right|\left|\combi{x}\right|+\left|b\right|\left|y\right|\le \sqrt{a^2+b^2}\sqrt{x^2+y^2}$|a||x|+|b||y|≤√a2+b2√x2+y2​

삼각부등식에 의하여

$\left|\combi{ax+by}\right|\le \left|\combi{a}\right|\left|\combi{x}\right|+\left|\combi{b}\right|\left|\combi{y}\right|$|ax+by|≤|a||x|+|b||y|​

이 성립하므로

$\left|\combi{ax+by}\right|\le \left|\combi{a}\right|\left|\combi{x}\right|+\left|\combi{b}\right|\left|\combi{y}\right|\le \sqrt{a^2+b^2}\sqrt{x^2+y^2}$|ax+by|≤|a||x|+|b||y|≤√a2+b2√x2+y2​

가 성립한다.