하양짱샘수학이야기

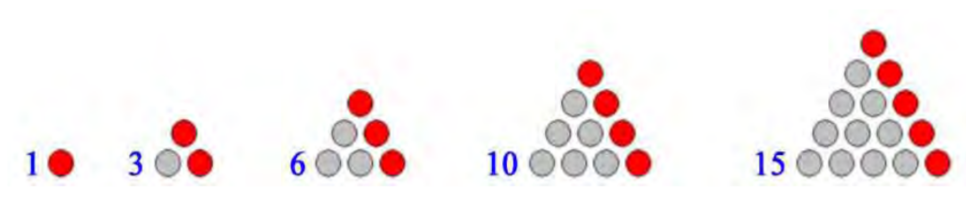
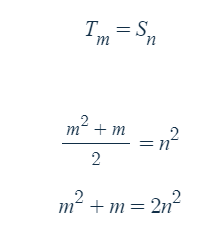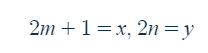다항식과 분수식을 통틀어서 유리식이라 하는데 유리식 중에서 분모에 문자가 있는 경우를 분수식이라 합니다.

유리식과 유리함수 단원에서는 주로 분수식을 다루게 되는데 유리식에 여러 가지 내용들이 나오게 됩니다.

분리형, 결합형, 부분분수, 비례식, 가비의 리 등등등...

그 중에서 부분분수에 대해서 알아보겠습니다.

부분분수란 하나의 분수를 두 개 이상의 분수의 합으로 나타내는 것을 말하는데, 교과서와 모든 수학 교재를 보면 다음과 같은 식이 유리식 부분분수 단원에서 나오게 됩니다.

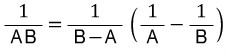
왜 간단한 식을 저렇게 복잡한 식으로 바꾸는것일까요?

하지만 간단한 예제 하나만 풀어보더라도 왜 그래야 하는지 쉽게 이해가 갈 것입니다.

또한 수열의 합 단원에서도 중요하게 쓰일 예정이니 꼭!꼭!꼭! 잘 알아두어야 합니다.

​

먼저 위 식을 증명해 보도록 하겠습니다.

다음과 같은 분수식이 있다고 해볼까요.

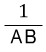
이제 이 식을 두 개의 분수의 합으로 나타내면 다음과 같이 되겠죠?

이 식이 성립한다면 우변의 식을 통분해서 계산하면 좌변의 식이 나와야 합니다.

여기서 특수한 b=-a인 상황을 생각해 봅시다.

즉, 하나의 분수를 분자의 절댓값은 같고 부호가 반대가 되는 두 분수의 합으로 나타내는 경우입니다.

이와 같이 되므로 결론은

이 되는 것입니다.

​

그럼 분자가 1이 아닌 경우를 생각해 봅시다.

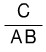
가 됩니다.

​

이제 이 식을 어떻게 활용하는지 간단히 알아보도록 하겠습니다.

의 값을 구하는 문제를 생각해볼까요.

물론 모두 60으로 통분하여 계산하면 간단하다.

그런데 만일 저러한 식이 연속으로 계속 더해져서 항이 100개정도 되는 분수의 합이라면 과연 통분으로 제한된 시간 내에 해결할 수 있을까?

위의 식을 다음과 같이 변형할 수 있습니다.

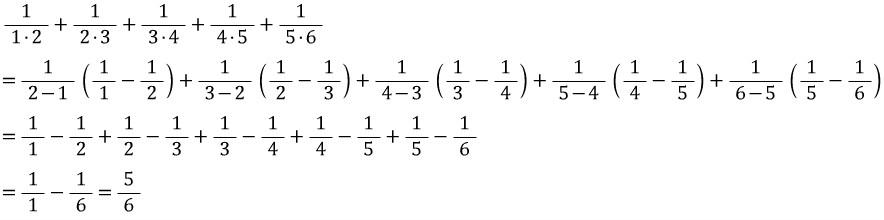
이웃한 항끼리 자연스럽게 소거가 됩니다.

부분분수는 이와 같이 분모가 두 식, 또는 두 수의 곱으로 되어있는 분수를 두 개의 분수의 합으로 바꾸면서 복잡한 계산을 간단히 만들어주는 역할을 합니다.

수학에서, 다각수(多角數, 영어: polygonal number)는 삼각수와 정사각수를 임의의 정다각형에까지 일반화하여 얻는 평면 도형수입니다.

​

고대 그리스 시대에 피타고라스학파는 “모든 것은 수이다”라 생각하여 모든 것을 수와 관련지어 생각했습니다. 심지어 도형도 숫자를 이용하여 표현하고 그 도형과 수와의 관계도 연구하였습니다.

​

기하학적으로 다각수는 정다각형에 배열된 공의 수를 나타냅니다. 주어진 다각수 바로 다음에 오는 다각수를 얻으려면 다각형의 이웃하는 두 변의 길이를 늘려 원래와 닮은 새로운 다각형으로 확장하면 됩니다. 이 경우 늘리려는 두 변에 각각 한 개의 공이 추가되며, 새로운 다각형의 남은 변을 만들기 위한 공들 역시 추가됩니다. 이렇게 추가되는 부분을 다각수의 그노몬(영어: gnomon)이라고 부릅니다. 대수학적으로, 다각수는 1에서 시작하는 자연수 공차의 등차 수열의 부분합을 나타내며, 그노몬은 이 등차 수열의 각 항에 대응합니다.

​

먼저 삼각수를 보겠습니다.

삼각수는 간단히 말하자면, 동일한 물건을 정삼각형 모양으로 배열해서 나타낼 수 있는 수입니다. 아래 그림과 같이 점의 수를 늘려가면서 정삼각형 모양의 배열을 계속해서 만들어 가는 것입니다. 이 때 각각의 정삼각형 모양의 배열을 만드는 점의 수로 이루어진 수들, 즉 1, 3, 6, 10, 15···에서 각각의 수가 삼각수에 해당하지요.

그럼 사각수는 어떤 것일까? 사각수는 말 그대로 정사각형 모양으로 배열해서 나타낼 수 있는 수랍니다. 아래 그림과 같이 점의 수를 늘려가면서 정사각형 모양의 배열을 계속해서 만들어 가는 것입니다. 이때 각각의 정사각형 모양의 배열을 만드는 점의 수로 이루어진 수들, 즉 1, 4, 9, 16, 25···에서 각각의 수가 사각수에 해당합니다.

위의 삼각수와 사각수를 이해했다면 오각수도 쉽게 이해할 수 있을 것입니다. 아래 그림과 같이 점의 수를 늘려가면서 정오각형 모양의 배열을 계속해서 만들어 가는 것입니다. 이 때 각각의 정오각형 모양의 배열을 만드는 점의 수로 이루어진 수들 1, 5, 12, 22, 35, ···에서 각각의 수가 오각수에 해당하는 것입니다.

다각수의 첫 항은 1로 모두 같습니다. 그리고 자연스럽게 다음과 같은 의문을 가질 수 있습니다. 첫 항을 제외하고 그 다음으로 삼각수와 사각수가 같아지는 항들을 찾을 수 있을까요? 일반항을 이용하면 8번째 삼각수가 36이므로 6번째 사각수와 같음을 알 수 있습니다. 이와 같은 방법으로 삼각수이면서 동시에 사각수인 수를 모두 찾을 수있을까요? 더 나아가 사각수이면서 동시에 오각수인 수를 찾을 수 있을까요? 또 그 개수는 얼마나 많을까요? 먼저 삼각수와 사각수를 생각해 보겠습니다.

​

m번째 삼각수와 n번째 사각수가 같다고 하면,

이 되고, 완전제곱식의 형태로 고쳐 봅니다.

여기서,

라고 하면,

(단, x, y >0 이고 x는 홀수, y 는 짝수)

의 자연수해를 구하는 문제로 바뀐다. 이 방정식을 펠의 방정식이라고 합니다.