
n개의 양수가 있을 때, 이들 수의 곱의 n제곱근 값을 기하평균이라고 합니다.
이름에서 알수 있듯 기하에서 유래 된것이라 볼 수 있습니다.
만약 세 개의 양수 a1, a2, a3가 주어졌다고 하면 세 수의 곱의 세제곱근값이 기하평균인 것이죠. 마찬가지로 n개의 양수 a1, a2, a3 … an이 있을 때, 이들 수의 곱의 n제곱근 값이 기하평균이 됩니다.
아래와 같이 가로 16m, 세로 2m, 높이 2m 크기의 직육면체가 있습니다.
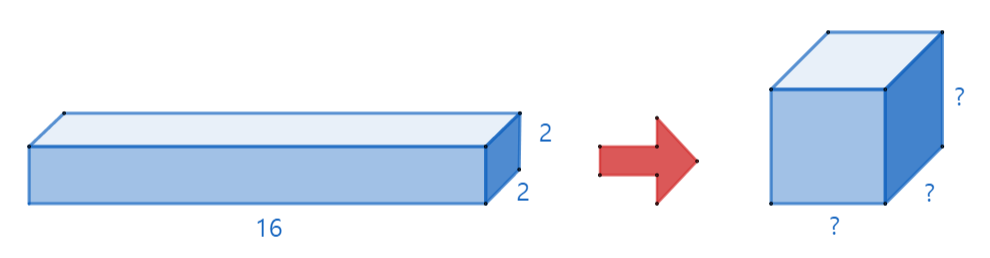
이 직육면체의 부피를 구하면 16x2x2=64㎥가 된다.
이 직육면체와 부피가 같은 정육면체의 한 모서리의 길이는 얼마가 되어야 할까요?
정육면체의 한 모서리의 길이를 x라고 하면, 정육면체의 부피는 x3이 됩니다.
이때 x의 값을 구하기 위해 방정식을 풀면 다음과 같습니다.
이렇게 한 모서리의 길이가 4m인 정육면체의 부피를 구하면, 4x4x4=64㎥로 직육면체의 부피와 동일함을 알 수 있습니다.
이때 정육면체의 한 모서리의 길이 4를 직육면체의 가로, 세로, 높이인 16, 2, 2라는 세 수의 기하평균이라 합니다.
기하평균은 넓이, 부피, 비율 등 곱으로 이루어지는 값들의 평균을 구하는 데 주로 사용됩니다.
직사각형의 넓이를 결정하는 가로와 세로의 길이의 기하평균은 동일한 넓이의 정사각형의 한 변의 길이를 의미하고, 직육면체의 부피를 결정하는 가로, 세로, 높이 세 값의 기하평균은 동일한 부피의 정육면체의 한 모서리의 길이를 의미합니다.
이를 응용하면 최근 3년간의 물가상승률의 기하평균을 구함으로써, 한 해의 평균적인 물가상승률을 구할 수 있습니다.
예를 들어 어떤 물건의 값이 처음에 1000원 이고, 첫 해에 10% 증가하고, 그 다음 해에 20% 증가하고, 그 다음 해에 15% 감소했다고 할 때 결과 값은 처음의 값 1000원에 1.1, 1.2, 0.85의 기하평균을 세 번 곱한 값이 됩니다.
1.1, 1.2, 0.85의 기하평균 (1.1 × 1.2 × 0.85)1/3 = 1.0391...이므로, 3년동안 평균 3.91%씩 증가한 셈입니다.
즉, 1000 × 1.1 × 1.2 × 0.85 = 1000 × (1.0391)3 입니다.
'확률과 통계 > 통계' 카테고리의 다른 글
| <하양짱샘수학과외>산술평균에 대해 알아보겠습니다. (0) | 2019.07.24 |
|---|---|
| <하양짱샘수학과외>평균이란 무엇인가? (0) | 2019.07.24 |
| <하양짱샘수학과외>하양여고 고3 문과 지필2차 수학 주요문제 풀이 10번 (0) | 2019.07.04 |
| <하양짱샘수학과외>하양여고 고3 문과 지필2차 수학 주요문제 풀이 4번 (0) | 2019.07.04 |