<하양짱샘수학>삼각형의 넓이구하기 ③ 변과 각의 크기를 이용

▶ 두변의 길이와 끼인각의 크기를 이용

-예각삼각형

 

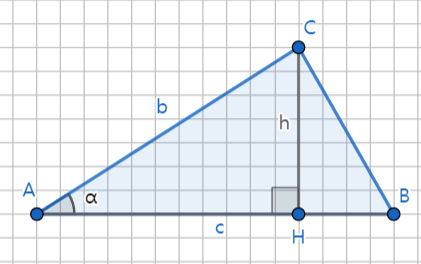
아래의 삼각형과 같이 선분 b,c그리고 그사이 끼인각 ∠α가 주어 졌을 때 △ABC의 넓이를 구하는 방법입니다.

 

중학3학년 삼각비과정에서 배우고

나면 자주 사용하는 방법으로 삼각형의 넓이를 구하는 다른 방법의 근간이 되는 방법입니다.

​

삼각형넓이가 사각형넓이의 반이 된다는 방법으로 유도된

$A=\frac{1}{2}ch$A=12​ch​

에서 높이h를 삼각함수로 구하는 방법입니다.

꼭지점 C에서 변c로 수선의 발을 내려 만나는 점을 H라하고 선분CH는 높이h가 됩니다.

 

$\sin \alpha =\frac{h}{b}$sinα=hb​​

$h=\sin \alpha \times b$h=sinα×b​

$A=\frac{1}{2}bc\sin \alpha $A=12​bcsinα​

​

한변의 길이와 양끝각의 크기를 이용

-예각삼각형

한변의 길이c와 양끝각 α,β가 주어 졌을 때

C에서 선분 AB에 수선의 발을 내리고 그 교점을 H라 하면, △ABC의 높이는 h가 됩니다.

$∠ACH=90-α,\ ∠BCH=90-β$∠ACH=90−α, ∠BCH=90−β​

가 됩니다.

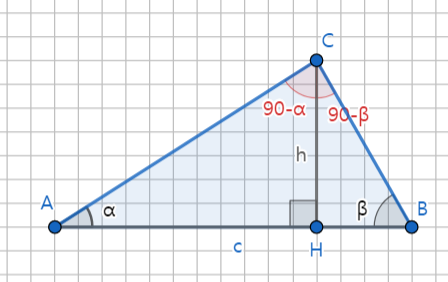
△ACH에서 기준각을∠ACH로 하면 선분CH는 밑변이 되고 선분AH는 높이가 됩니다.

△BCH에서 기준각을 ∠BCH로 하면 선분BH는 밑변이 되고 선분BH는 높이가 됩니다.

 

$\tan \left(90-\alpha \right)=\frac{\overline {AH}}{h}$tan(90−α)=AHh​​

$\overline {AH}=h\tan \left(90-\alpha \right)$AH=htan(90−α)​

$\tan \left(90-\beta \right)=\frac{\overline {BH}}{h}$tan(90−β)=BHh​​

$\overline {BH}=h\tan \left(90-\beta \right)$BH=htan(90−β)​

$$​

△ABC에서

 

$\overline {AB}=\overline {AH}+\overline {BH}$AB=AH+BH​

$=h\tan \left(90-\alpha \right)+h\tan \left(90-\beta \right)$=htan(90−α)+htan(90−β)​

$=h\left\{\tan \left(90-\alpha \right)+\tan \left(90-\beta \right)\right\}$=h{tan(90−α)+tan(90−β)}​

$\therefore \ h=\frac{\overline {AB}}{\left\{\combi{\tan \left(90-\alpha \right)+\tan \left(90-\beta \right)}\right\}}$∴ h=AB{tan(90−α)+tan(90−β)}​​

∴△ABC의 넓이

 

$A=\frac{1}{2}c\frac{c}{\left\{\combi{\tan \left(90-\alpha \right)+\tan \left(90-\beta \right)}\right\}}$A=12​cc{tan(90−α)+tan(90−β)}​​

$=\frac{c^2}{2\left\{\combi{\tan \left(90-\alpha \right)+\tan \left(90-\beta \right)}\right\}}$=c22{tan(90−α)+tan(90−β)}​​

두변의 길이와 끼인각의 크기를 이용

-둔각삼각형

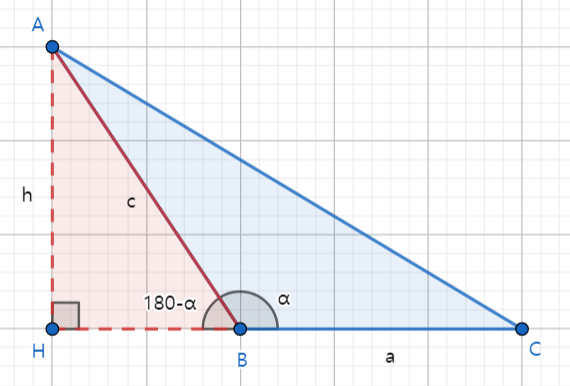
예각삼각형과 달리 둔각삼각형에서는 두변의 길이와 끼인각의 크기를 알 때, A에서 내린 수선이 삼각형의 바깥쪽에 내려져 선분BC의 연장선과 만나게 됩니다.

그 교점을 H라 하면, 선분AH가 △ABC의 높이가 됩니다.

삼각형의 넓이는 둔각삼각형이든 예각 삼각형이든 상관없이 밑변의 길이와 높이만 이용해 구할 수 있습니다.

이 내용은 앞에서 공부했던 삼각형 넓이 구하는 방법은 <하양짱샘수학>삼각형의 넓이구하기 ①밑변의 길이와 높이를 이용에서 공부한 바 있습니다.

​

둔각△ABC에서 선분AH를 구하면 넓이를 구할 수 있습니다.

선분AH는 △ABH에서 삼각비를 이용하면 구할수 있겠죠?

$\sin \left(180-\alpha \right)=\frac{\overline {BH}}{\overline {AH}}=\frac{h}{c}$sin(180−α)=BHAH​=hc​​

$h=c\sin \left(180-\alpha \right)$h=csin(180−α)​

$A=\frac{1}{2}ac\sin \left(180-\alpha \right)$A=12​acsin(180−α)​

한변의 길이와 양끝각의 크기를 이용

-둔각삼각형

위의 경우와 마찬가지로 점A에서 선분BC의 연장선에 수선을 내립니다.

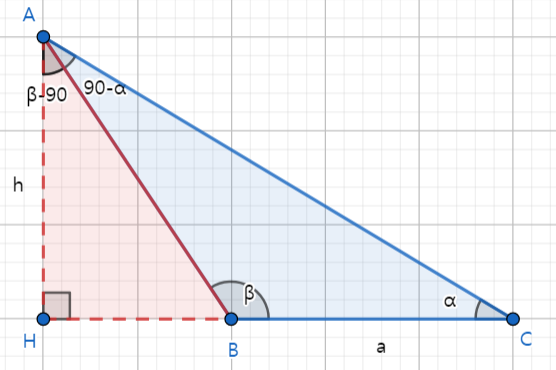
△AHC에서

 

$\angle CAH=90\cir -\alpha $∠CAH=90°−α​

$\tan \left(90\cir -\alpha \right)=\frac{\overline {CH}}{\overline {AH}}=\frac{\overline {CH}}{h}$tan(90°−α)=CHAH​=CHh​​

$\overline {CH}=h\tan \left(90\cir -\alpha \right)$CH=htan(90°−α)​

△AHB에서

 

$\angle ABH=180\cir -\beta $∠ABH=180°−β​

$\angle BAH=180\cir -90\cir -\left(180\cir -\beta \right)$∠BAH=180°−90°−(180°−β)​

$=\beta -90\cir $=β−90°​

$$​

$\tan \left(\beta -90\cir \right)=\frac{\overline {BH}}{\overline {AH}}=\frac{\overline {BH}}{h}$tan(β−90°)=BHAH​=BHh​​

$\overline {BH}=h\tan \left(\beta -90\cir \right)$BH=htan(β−90°)​

$$​

$\overline {BC}=\overline {CH}-\overline {BH}$BC=CH−BH​

$\ \ \ \ a=h\tan \left(90\cir -\alpha \right)-h\tan \left(\beta -90\cir \right)$    a=htan(90°−α)−htan(β−90°)​

$\ \ \ \ \ =h\left\{\combi{\tan \left(90\cir -\alpha \right)-\tan \left(\beta -90\cir \right)}\right\}$     =h{tan(90°−α)−tan(β−90°)}​

$h=\frac{a}{\left\{\tan \left(90\cir -\alpha \right)-h\tan \left(\beta -90\cir \right)\right\}}$h=a{tan(90°−α)−htan(β−90°)}​​

$$​

∴ △ABC의 넓이

 

 

$A=\frac{1}{2}a\frac{a}{\left\{\tan \left(90\cir -\alpha \right)-h\tan \left(\beta -90\cir \right)\right\}}$A=12​aa{tan(90°−α)−htan(β−90°)}​​

$=\frac{a^2}{2\left\{\tan \left(90\cir -\alpha \right)-h\tan \left(\beta -90\cir \right)\right\}}$=a22{tan(90°−α)−htan(β−90°)}​​